The tidyverse is a collection of R packages developed by RStudio’s chief scientist Hadley Wickham. These packages work well together as part of larger data analysis pipeline. To learn more about these tools and how they work together, read R for data science. For newcomers to R, please check out my previous tutorial for Storybench: Getting Started with R in RStudio Notebooks.

The following tutorial will introduce some basic functions in tidyverse for structuring and analyzing datasets. This is the first in a three-part series on cleaning data to visualize it in R using the tidyverse.

Load the packages

First, install tidyverse and then load tidyverse and magrittr.

suppressWarnings(suppressMessages(install.packages("tidyverse")))
suppressWarnings(suppressMessages(library(tidyverse)))
suppressWarnings(suppressMessages(library(magrittr)))

Learn the “pipe”

We’ll be using the “pipe” throughout this tutorial. The pipe makes your code read more like a sentence, branching from left to right. So something like this: f(x)becomes this: x %>% f and something like this: h(g(f(x)))becomes this: x %>% f %>% g %>% h

The “pipe” and is from the magrittr package. Read about using it here.

What is tidy data?

“Tidy data” is a term that describes a standardized approach to structuring datasets to make analyses and visualizations easier. If you’ve worked with SQL and relational databases, you’ll recognize most of these concepts. Hadley Wickham took a lot of the technical jargon from Edgar F. Codd’s normal form and applied it to a single data table. More importantly, he translated these principles into terms just about anyone doing data analysis should be able to recognize and understand.

The core tidy data principles

There are three principles for tidy data:

1. Variable make up the columns
2. Observations make up the rows
3. Values go into cells

The third principle is almost a given if you’ve handled the first two, so we will focus on these.

A hypothetical clinical trial to explain variables

A variable is any measurement that can take multiple values. Depending on the field a dataset comes from, variables can be referred to as an independent or dependent variables, features, predictors, outcomes, targets, responses, or attributes.

Variables can generally fit into three categories: fixed variables (characteristics that were known before the data were collected), measured variables (variables containing information captured during a study or investigation), and derived variables (variables that are created during the analysis process from existing variables).

Here’s an example: Suppose clinicians were testing a new anti-hypertensive drug. They recruit 30 patients, all of whom are being treated for hypertension, and divide them randomly into three groups. The clinician gives one third of the patients the drug for eight weeks, another third gets a placebo, and the final third gets care as usual. At the beginning of the study, the clinicians also collect information about the patients. These measurements included the patient’s sex, age, weight, height, and baseline blood pressure (pre BP).

For patients in this hypothetical study, suppose the group they were randomized to (i.e the drug, control, or placebo group), would be considered a fixed variable. The measured pre BP (and post BP) would be considered the measured variables.

Suppose that after the trial was over–and all of the data were collected–the clinicians wanted a way of identifying the number of patients in the trial with a reduced blood pressure (yes or no)? One way is to create a new categorical variable that would identify the patients with post BP less than 140 mm Hg (1 = yes, 0 = no). This new categorical variable would be considered a derived variable.

The data for the fictional study I’ve described also contains an underlying dimension of time. As the description implies, each patient’s blood pressure was measured before and after they took the drug (or placebo). So these data could conceivably have variables for date of enrollment (the date a patient entered the study), date of pre blood pressure measurement (baseline measurements), date of drug delivery (patient takes the drug), date of post blood pressure measurement (blood pressure measurement taken at the end of the study).

What’s an observation?

Observations are the unit of analysis or whatever the “thing” is that’s being described by the variables. Sticking with our hypothetical blood pressure trial, the patients would be the unit of analysis. In a tidy dataset, we would expect each row to represent a single patient. Observations are a bit like nouns, in a sense that pinning down an exact definition can be difficult, and it often relies heavily on how the data were collected and what kind of questions you’re trying to answer. Other terms for observations include records, cases, examples, instance, or samples.

What is the data table?

Tables are made up of values. And as you have probably already guessed, a value is the thing in a spreadsheet that isn’t a row or a column. I find it helpful to think of values as physical locations in a table – they are what lie at the intersection of a variable and an observation.

For example, imagine a single number, 75, sitting in a table.

	Column 1	Column 2
Row 1
Row 2		75

We could say this number’s location is the intersection of Column 2 and Row 2, but that doesn’t tell us much. The data, 75, is meaningless sitting in a cell without any information about what it represents. A number all alone in a table begs the question, “seventy-five what?”

This is why thinking of a table as being made of variables (in the columns) and observations (in the rows) helps get to the meaning behind the values in each cell. After adding variable (column) and observation (row) names, we can see that this 75 is the pre diastolic blood pressure (Pre_Dia_BP) for patient number 3 (patient_3).

	Col 1	Pre_Dia_BP
Row 1
patient_3		75

It’s also worth pointing out that this same information could be presented in another way:

	meas_type	Dia_BP
Row 1
patient_3	pre	75

This arrangement is displaying the same information (i.e. the pre diastolic blood pressure for patient number 3), but now the column meas_type is containing the information on which blood pressure measurement the 75 represents (pre). Which one is tidy? In order to answer this, we will build a pet example to establish some basic tidying terminology.

How the “tibble” is better than a table

We will use the call below to create a key-value pair reference tibble. tibbles are an optimized way to store data when using packages from the tidyverse and you should read more about them here.

We are going to build a tibble from scratch, defining the columns (variables), rows (observations), and contents of each cell (value). By doing this, we’ll be able to keep track of what happens as we rearrange these data. The goal of this brief exercise is to make key-value pairs easier to see and understand.

Our new object (key_value) is built with the following underlying logic.

1. Rows are numbered with a number (1–3) and an underscore (_), and always appear at the front of a value.
2. Columns are numbered with an underscore (_) and a number (1–3), and always appear at the end of a value.

library(tidyr)
library(tibble)

key_value <- tribble(
     ~row, ~key1, ~key2, ~key3, # These are the names of the columns (indicated with ~)
     "1", "1_value_1","1_value_2","1_value_3", # Row 1
     "2", "2_value_1", "2_value_2", "2_value_3", # Row 2
     "3", "3_value_1", "3_value_2", "3_value_3" # Row 3
)
key_value

So, the value for key1 and row = 1 is 1_value_1; The value for key2 and row = 2 is 2_value_2; and so on.

The first number #_ represents the row (observation) position, the trailing number _# represents the key_ column (variable) position.

Using the tidyr package

tidyr is a package from the tidyverse that helps you structure (or re-structure) your data so its easier to visualize and model. Here is a link to the tidyr page. Tidying a data set usually involves some combination of either converting rows to columns (spreading), or switching the columns to rows (gathering).

We can use our key_value object to explore how these functions work.

Using gather

“Gather takes multiple columns and collapses into key-value pairs, duplicating all other columns as needed. You use gather() when you notice that you have columns that are not variables.” That’s how tidyverse defines gather.

Let’s start by gathering the three key columns into a single column, with a new column value that will contain all their values.

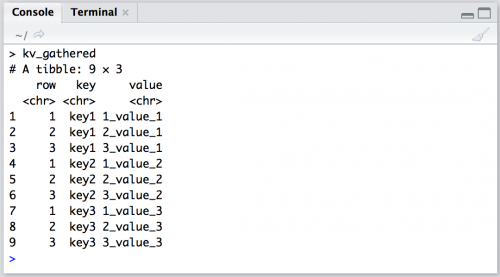
kv_gathered <- key_value %>% 
     gather(key, # this will be the new column for the 3 key columns
            value, # this will contain the 9 distinct values
            key1:key3, # this is the range of columns we want gathered
            na.rm = TRUE # handles missing
            )
kv_gathered

Notice the structure:

• The new key column is now 9 rows, with the values from the three former key1, key2, and key3 columns.
• The value column contains all the content from the cells at each intersection of row and the key1, key2, and key3 columns

I call this arrangement of data "stacked." Wickham refers to this as indexed. But the important takeaway is that we’ve used gather() to scoop up the data that was originally scattered across three columns and placed them into two columns: key and value.

Using key-value pairs

Key-value pairs pair up keys and values. This means when we specified key as the name of the new column, the command took the three previous key columns and stacked them in it. Then we specified value as the name of the new column with their corresponding value pair.

What about the row column? We left this column out of the call because we want it to stay in the same arrangement (i.e. 1,2,3). When the key and value columns get stacked, these rows get repeated down the column,

Nothing was lost in the process, either. I can still look at row:3,key:2 and see the resulting value 3_value_2.

Using spread

Now we’ll spread the key and value columns back into their original arrangement (three columns of key_1, key_2, & key_3). The spread description reads: “Spread a key-value pair across multiple columns.”

kv_spreaded <- kv_gathered %>% 
     spread(
          key, 
          value
          )
kv_spreaded

Spread moved the values that were stacked in two columns (key and value) into the three distinct key_ columns.




The key-value pairs are the indexes we can use to rearrange the data to make it tidy.

Which version of the key_value is tidy? We stated that tidy data means, “one variable per column, one observation per row,” so the arrangement that satisfied this condition is the key_gathered data set. But I want to stress that without knowledge of what these variables and observations actually contain, we can’t really know if these data are tidy.